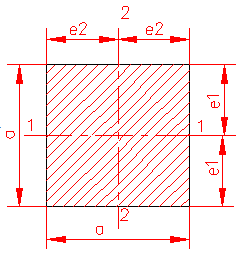
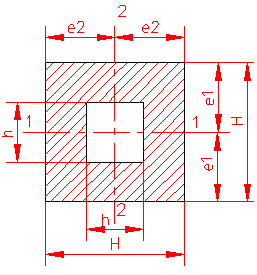
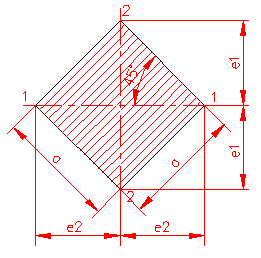
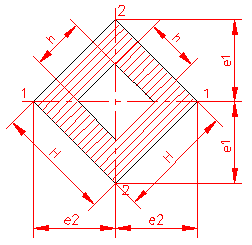
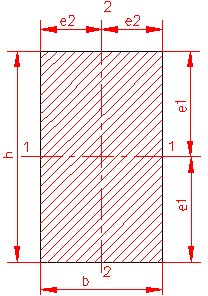
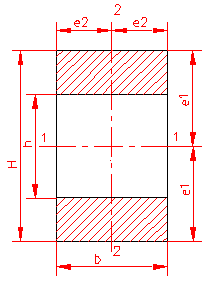
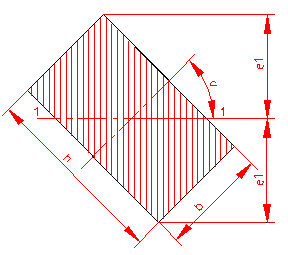
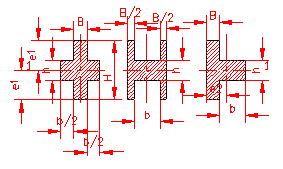
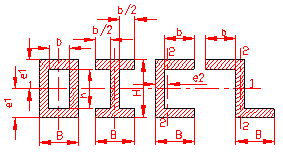
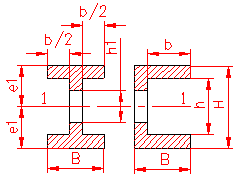
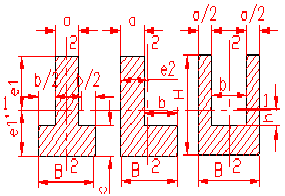
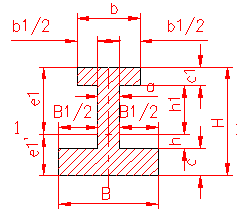
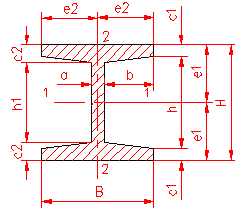
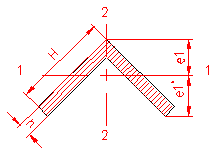
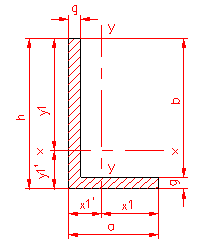
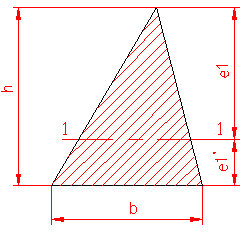
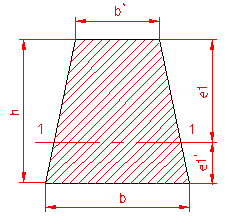
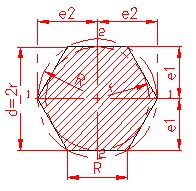
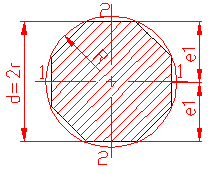
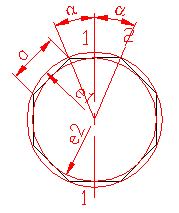
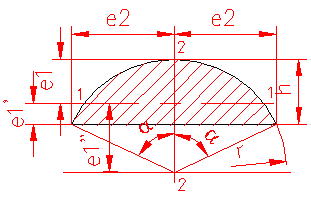
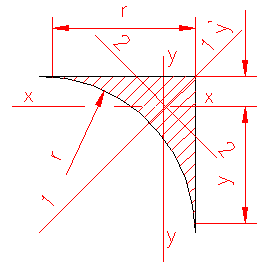
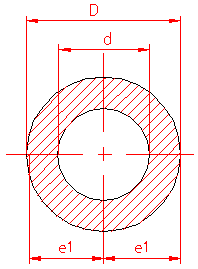
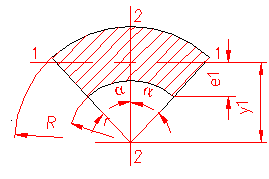
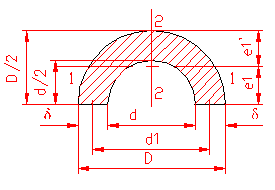
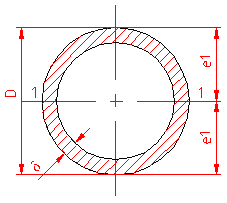
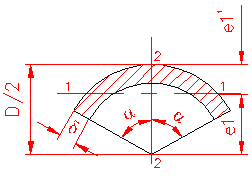
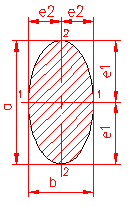
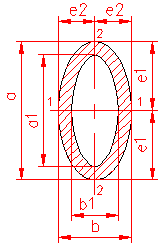
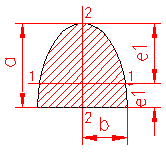
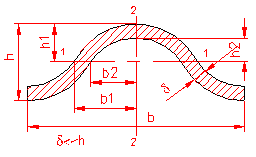
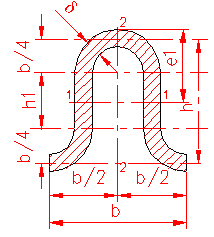
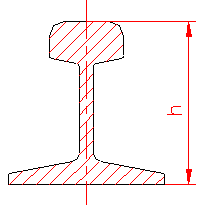
MOMENT INERTIE - SELECTATI SCHEMA DORITA
In definirea răspunsului elementelor de construcţii de tipul barelor la acţiunea forţelor exterioare, privind forţele interioare si deformaţiile care se produc in acestea, alături de proprietăţile fizice ale materialelor din care sunt alcătuite si dimensiunile acestora, intra si unele mărimi legate direct de forma si dimensiunile secţiunilor transversale ale barelor numite caracteristici geometrice ale sectiunilor.
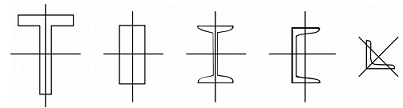
Daca se considera secţiunea transversala compusa dintr-o infinitate de arii elementare dA, rezulta:
Aria secţiunii:
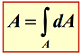
unde indicele A la semnul de integrare specifica extinderea integralei pe toata secţiunea.
Momentele statice fata de axa y, respectiv z:
reprezintă suma produselor ariilor elementare dA cu distanta la axa corespunzătoare (y sau z).
Daca se considera secţiunea transversala compusa dintr-o infinitate de arii elementare dA, rezulta:
Daca se notează cu yG si zG coordonatele centrului de masa sau de greutate ale secţiunii rezulta:
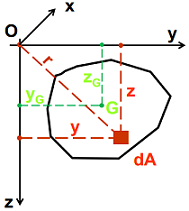
Observatii. Din relaţia de mai sus se deduce ca momentul static al secţiunii fata de o axa care trece prin centrul de greutate al acestei secţiuni este nul. Axele de coordonate care trec prin centrul de greutate al secţiunii se numesc axe centrale, sistemele de axe rectangulare yOz cu originea in centrul de greutate al secţiunii numindu-se sisteme de axe centrale.
In cazul unei secţiuni compuse din mai multe secţiuni simple Ai, pentru care sunt cunoscute coordonatele yi si zi ale centrului de greutate Gi, coordonatele centrului de masa sau de greutate ale întregii secţiuni rezulta:
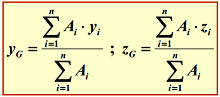
Observatii.
Ariile secţiunilor transversale plane au dimensiunea (L2), si se măsoară in mm2, cm2, m2...
Momentele statice ale secţiunilor transversale plane au dimensiunea (L3), si se măsoară in mm3, cm3, m3...
Se numeşte moment de inerţie axial al figurii plane, de arie A, in raport cu o axa din planul sau, suma produselor elementelor de arie dA cu pătratele distantelor lor la axa considerata. In raport cu axele Oy si Oz momentele de inerţie sunt:
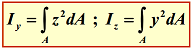
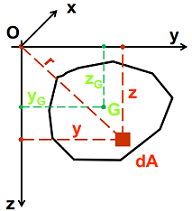
Suma produselor elementelor de arie dA cu distantele lor la un sistem de axe rectangular Oyz se numeşte moment de inerţie centrifugal al figurii plane in raport cu axele Oyz.
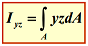
Moment de inerţie polar al unei figuri plane, in raport cu un punct (pol) din planul figurii, este suma produselor elementelor de arie dA cu pătratele distantelor lor la acel punct.
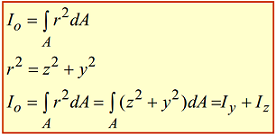
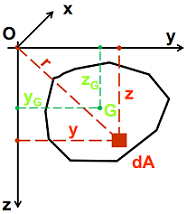
Suma momentelor de inerţie axiale in raport cu axele rectangulare cu aceeaşi origine O reprezintă un invariant la rotirea sistemului de axe.
Momentele de inerţie (axiale, centrifugale si polare) au dimensiunea (L4), si se măsoară in mm4, cm4, m4….
Sectiunea 1
Sectiunea 2
Sectiunea 3
Sectiunea 4
Sectiunea 5
Sectiunea 6
Sectiunea 7
Sectiunea 8
Sectiunea 9
Sectiunea 10
Sectiunea 11
Sectiunea 12
Sectiunea 13
Sectiunea 14
Sectiunea 15
Sectiunea 16
Sectiunea 17
Sectiunea 18
Sectiunea 19
Sectiunea 20
Sectiunea 21
Sectiunea 22
Sectiunea 23
Sectiunea 24
Sectiunea 25
Sectiunea 26
Sectiunea 27
Sectiunea 28
Sectiunea 29
Sectiunea 30
Sectiunea 31
Sectiunea 32
Sectiunea 33
Sectiunea 34
Sectiunea 35
Sectiunea 36
Sectiunea 37
